6 Chapter 3 Lab

6.1 Autoregressive model (AR)

AR(p) process is correlation with lagged values of the data itself.

\[ X_t-\mu = \alpha \cdot (X_{t-1}-\mu)+Noise_t\]

Some simulation examples down below. Note how the coefficent \(\phi\) affects the look of the graph:

x <- arima.sim(model = list(ar = 0.5), n = 100)

# Simulate an AR model with 0.9 slope
y <- arima.sim(model = list(ar = 0.9), n = 100)

# Simulate an AR model with -0.75 slope
z <- arima.sim(model = list(ar = -0.75), n = 100)

plot.ts(cbind(x, y, z))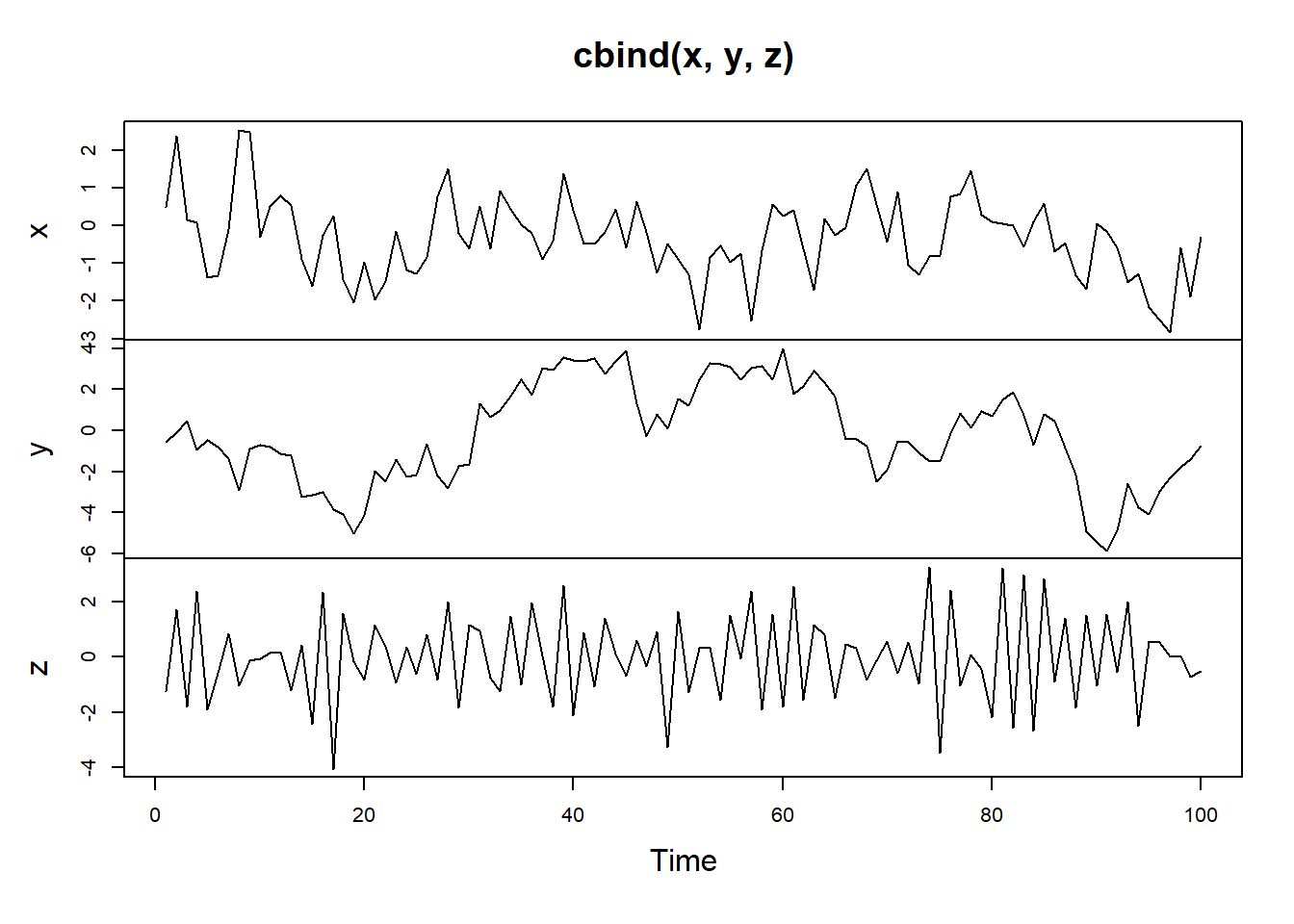

AR(1) model with slope \(\alpha=0.9\) creates a obvious trend while the negative slope creates a zic-zac pattern.

par(mfrow = c(3,1))

# Plot your simulated data
acf(x)
acf(y)
acf(z)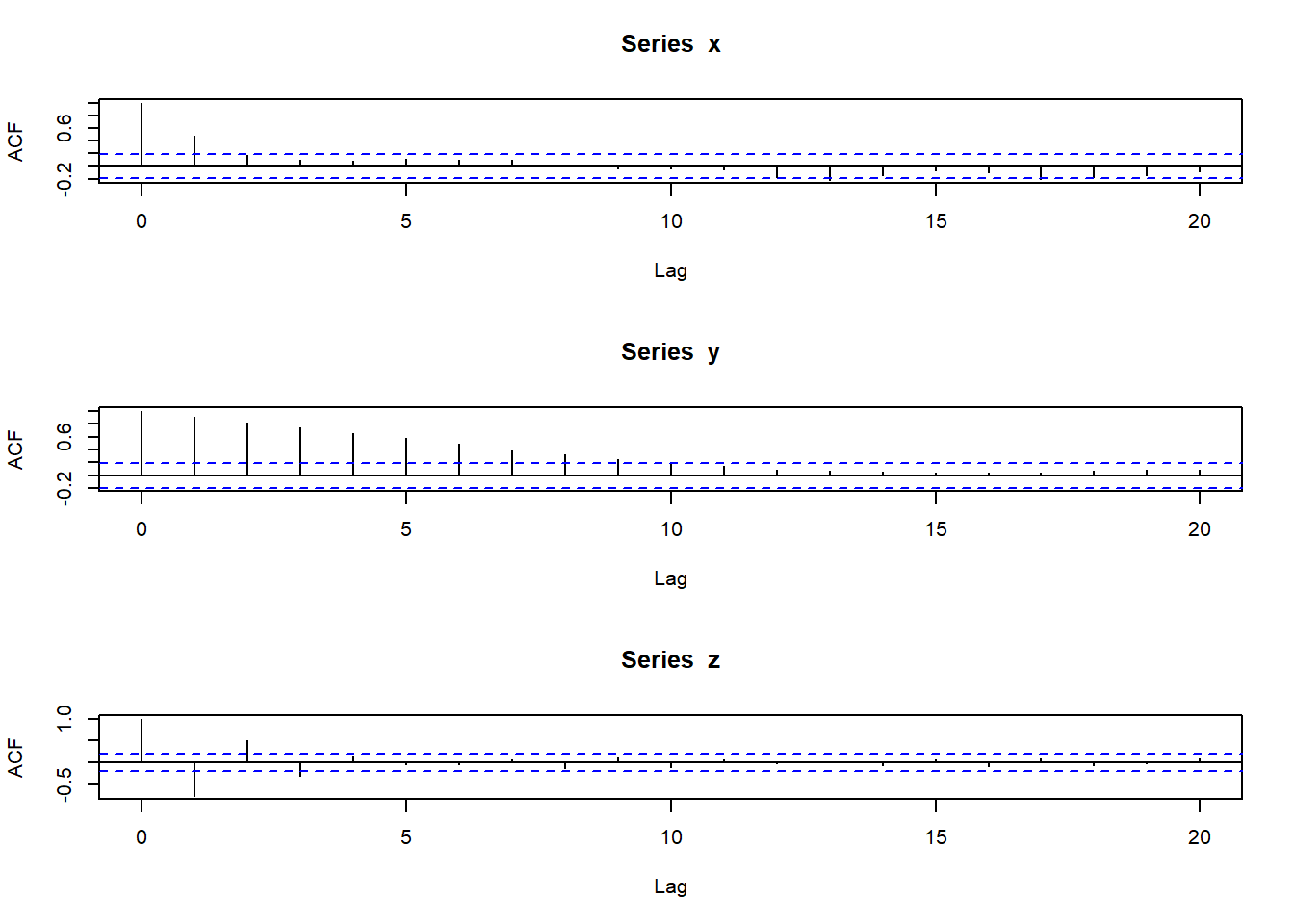

The ACF plots tell a lot about each time plot:

1. Strong short-term positive correlation in early lags (1 and 2)

2. Strong short-term positive correlation in early lags up to lag of 5

3. Strong short-term negative correlation in early lags up to lag of 5

The PACF will tell us what AR(p) model would be appropriate for fitting this data

par(mfrow = c(3,1))

# Plot your simulated data
pacf(x)
pacf(y)
pacf(z)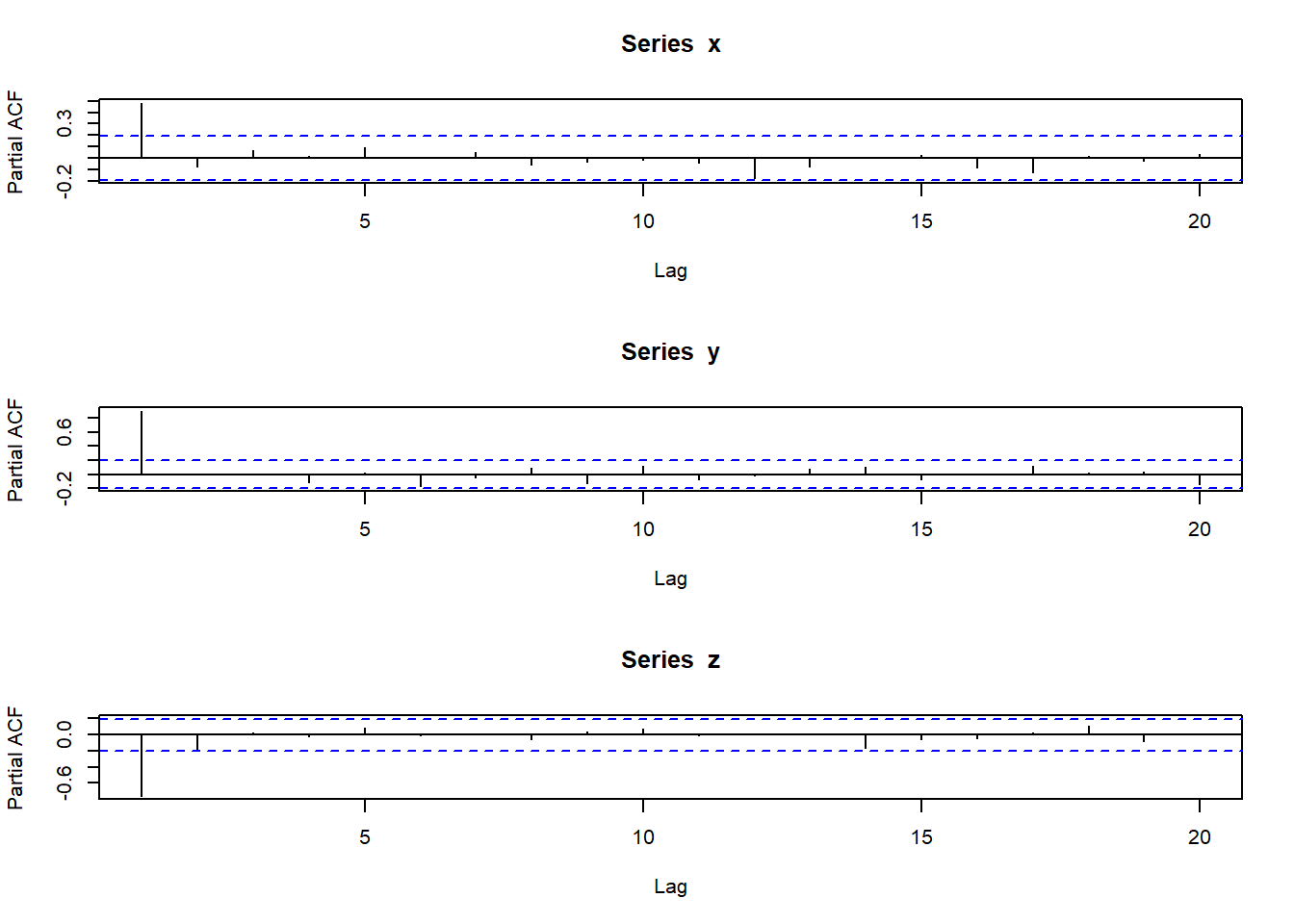

The PACF plots tell us that a AR(1) model would be appropriate for all 3 data. This is expected since we used AR(1) models to generate these data.

6.2 Chicken Price

6.3 Chicken price

library(astsa)

# Plot differenced chicken
plot(diff(chicken))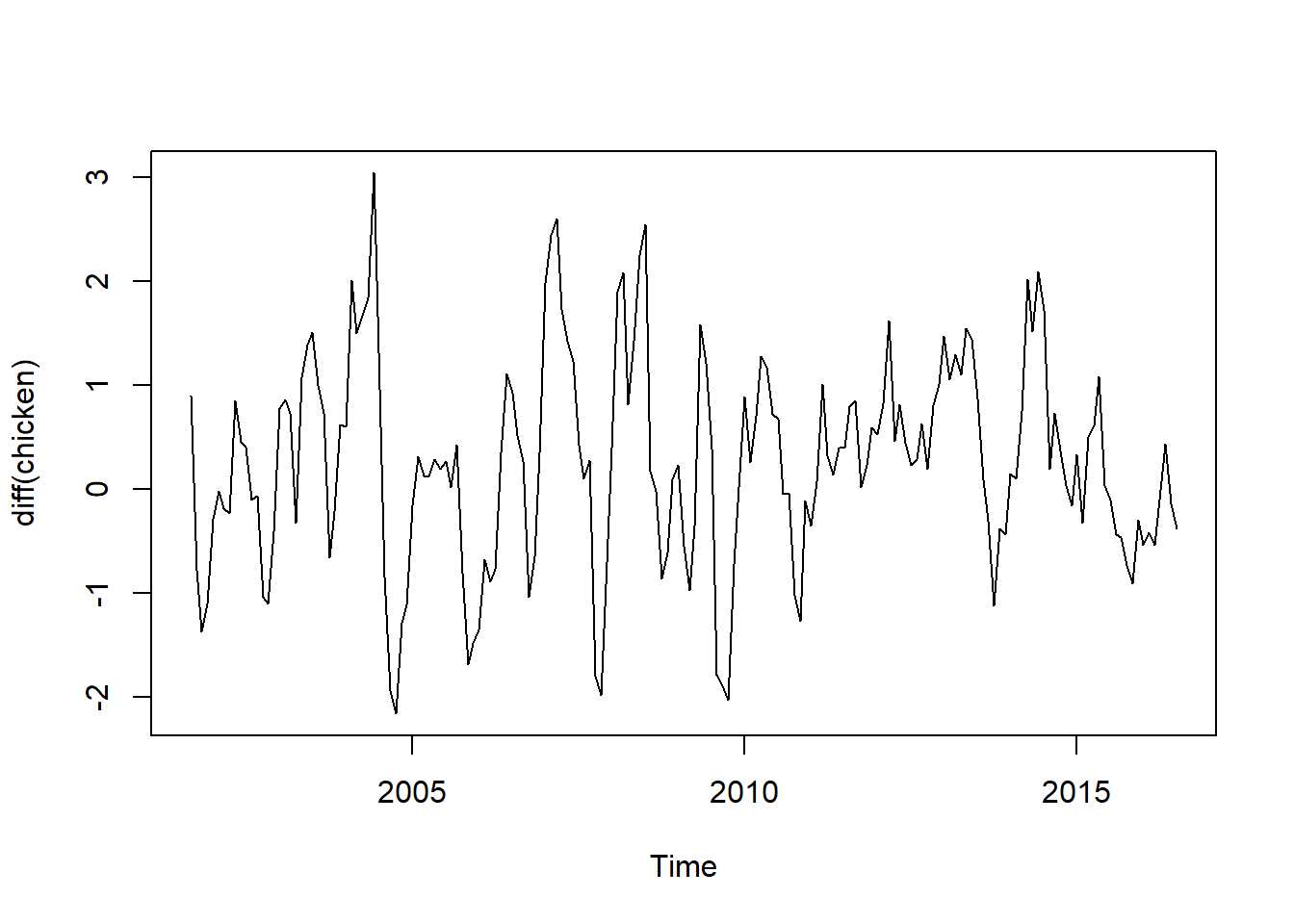 

# Plot P/ACF pair of differenced data to lag 60
acf2(diff(chicken), max.lag = 60)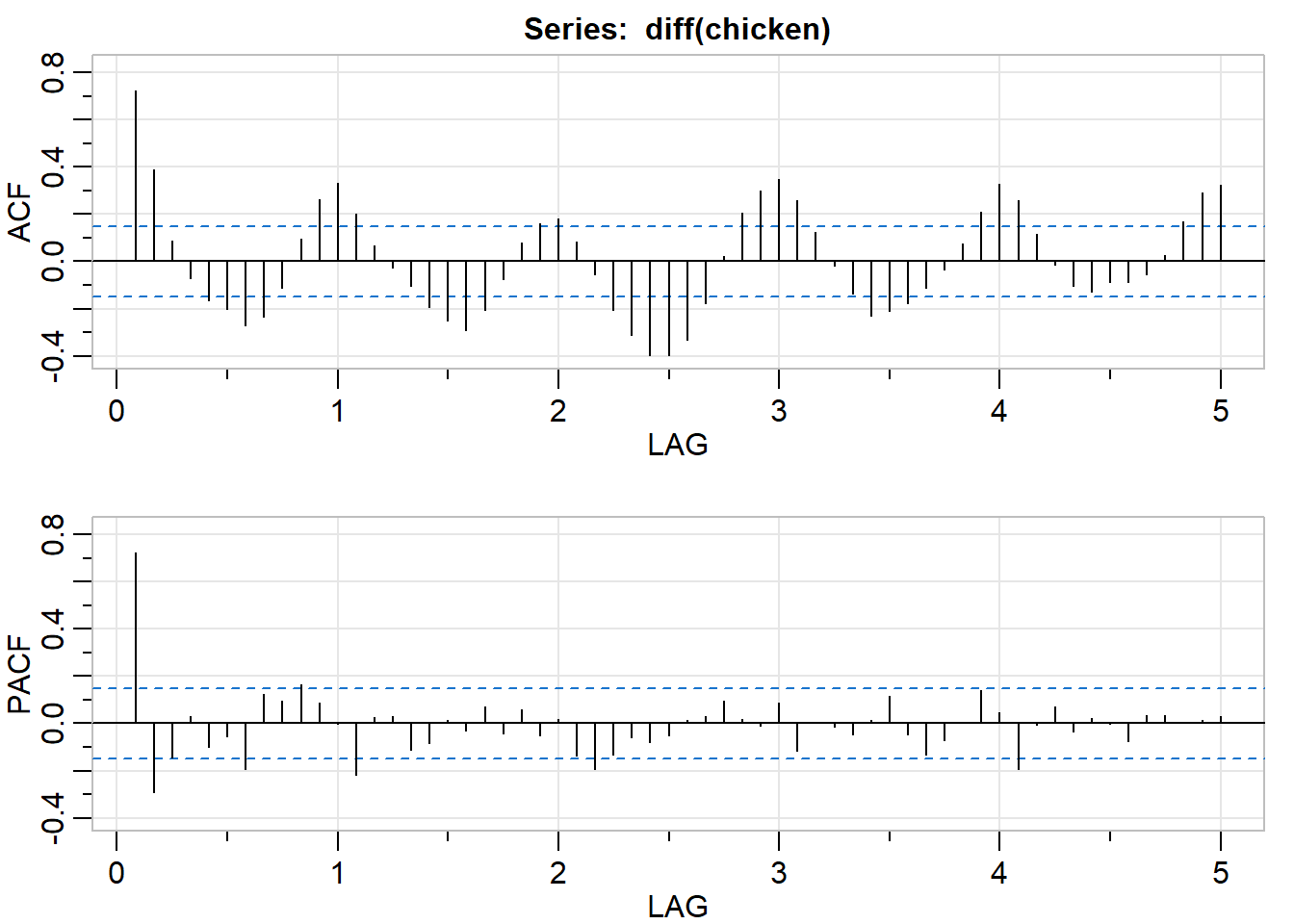

##      [,1]  [,2]  [,3]  [,4]  [,5]  [,6]  [,7]  [,8]  [,9] [,10] [,11] [,12]
## ACF  0.72  0.39  0.09 -0.07 -0.16 -0.20 -0.27 -0.23 -0.11  0.09  0.26  0.33
## PACF 0.72 -0.29 -0.14  0.03 -0.10 -0.06 -0.19  0.12  0.10  0.16  0.09  0.00
##      [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24]
## ACF   0.20  0.07 -0.03 -0.10 -0.19 -0.25 -0.29 -0.20 -0.08  0.08  0.16  0.18
## PACF -0.22  0.03  0.03 -0.11 -0.09  0.01 -0.03  0.07 -0.04  0.06 -0.05  0.02
##      [,25] [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36]
## ACF   0.08 -0.06 -0.21 -0.31 -0.40 -0.40 -0.33 -0.18  0.02  0.20  0.30  0.35
## PACF -0.14 -0.19 -0.13 -0.06 -0.08 -0.05  0.01  0.03  0.10  0.02 -0.01  0.09
##      [,37] [,38] [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48]
## ACF   0.26  0.13 -0.02 -0.14 -0.23 -0.21 -0.18 -0.11 -0.03  0.08  0.21  0.33
## PACF -0.12  0.01 -0.01 -0.05  0.02  0.12 -0.05 -0.13 -0.07  0.01  0.14  0.05
##      [,49] [,50] [,51] [,52] [,53] [,54] [,55] [,56] [,57] [,58] [,59] [,60]
## ACF   0.26  0.12 -0.01 -0.11 -0.13 -0.09 -0.09 -0.06  0.03  0.17  0.29  0.32
## PACF -0.20 -0.01  0.07 -0.04  0.02  0.00 -0.08  0.03  0.04  0.00  0.01  0.03

# Fit ARIMA(2,1,0) to chicken - not so good
sarima(chicken, p = 2, d = 1, q = 0)

## initial  value 0.001863 
## iter   2 value -0.156034
## iter   3 value -0.359181
## iter   4 value -0.424164
## iter   5 value -0.430212
## iter   6 value -0.432744
## iter   7 value -0.432747
## iter   8 value -0.432749
## iter   9 value -0.432749
## iter  10 value -0.432751
## iter  11 value -0.432752
## iter  12 value -0.432752
## iter  13 value -0.432752
## iter  13 value -0.432752
## iter  13 value -0.432752
## final  value -0.432752 
## converged
## initial  value -0.420883 
## iter   2 value -0.420934
## iter   3 value -0.420936
## iter   4 value -0.420937
## iter   5 value -0.420937
## iter   6 value -0.420937
## iter   6 value -0.420937
## iter   6 value -0.420937
## final  value -0.420937 
## converged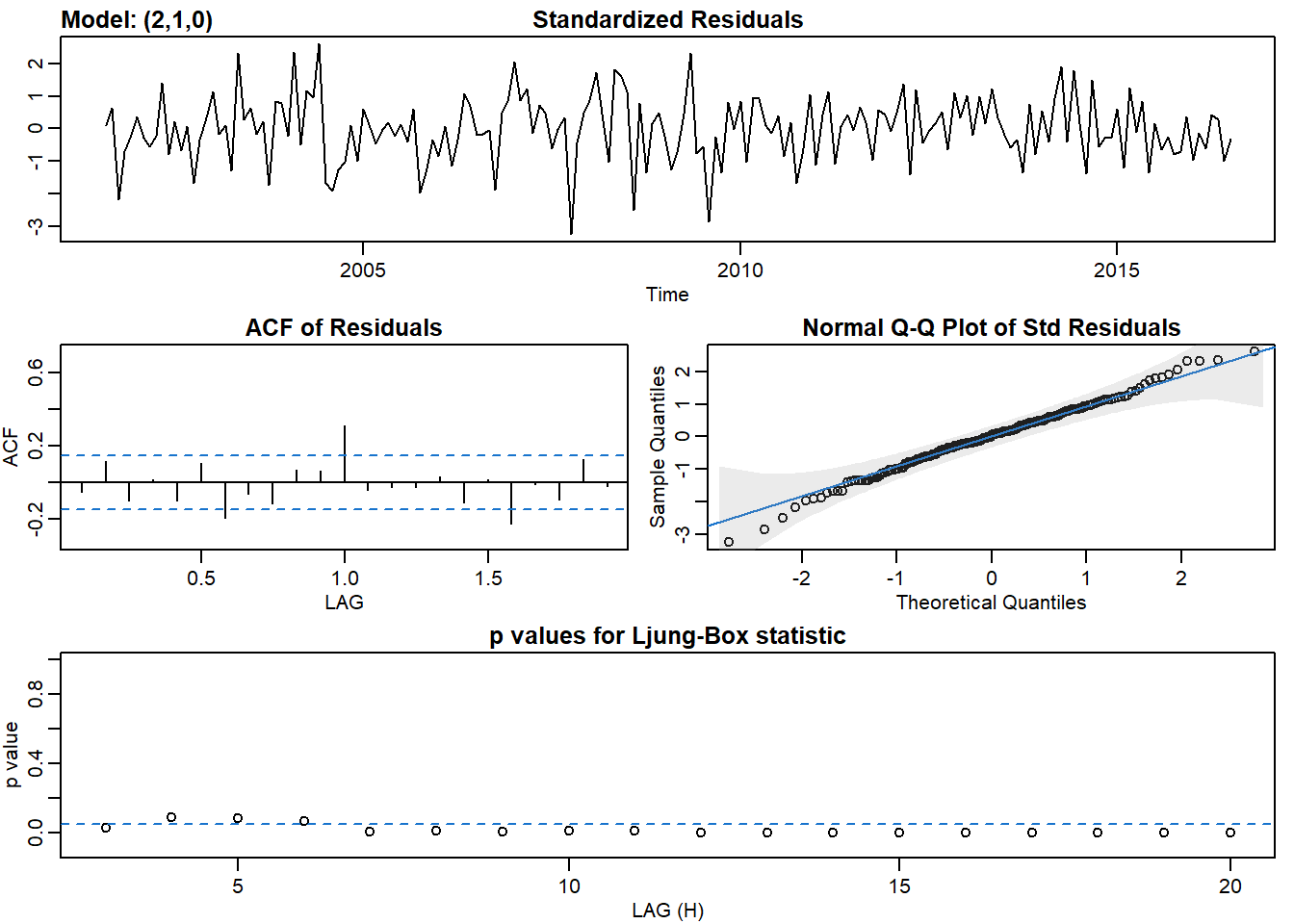

## $fit
## 
## Call:
## stats::arima(x = xdata, order = c(p, d, q), seasonal = list(order = c(P, D, 
##     Q), period = S), xreg = constant, transform.pars = trans, fixed = fixed, 
##     optim.control = list(trace = trc, REPORT = 1, reltol = tol))
## 
## Coefficients:
##          ar1      ar2  constant
##       0.9494  -0.3069    0.2632
## s.e.  0.0717   0.0718    0.1362
## 
## sigma^2 estimated as 0.4286:  log likelihood = -178.64,  aic = 365.28
## 
## $degrees_of_freedom
## [1] 176
## 
## $ttable
##          Estimate     SE t.value p.value
## ar1        0.9494 0.0717 13.2339  0.0000
## ar2       -0.3069 0.0718 -4.2723  0.0000
## constant   0.2632 0.1362  1.9328  0.0549
## 
## $AIC
## [1] 2.040695
## 
## $AICc
## [1] 2.041461
## 
## $BIC
## [1] 2.111922

# Fit SARIMA(2,1,0,1,0,0,12) to chicken - that works
sarima(chicken, p = 2, d = 1, q = 0, P = 1, D = 0, Q = 0, S = 12)

## initial  value 0.015039 
## iter   2 value -0.226398
## iter   3 value -0.412955
## iter   4 value -0.460882
## iter   5 value -0.470787
## iter   6 value -0.471082
## iter   7 value -0.471088
## iter   8 value -0.471090
## iter   9 value -0.471092
## iter  10 value -0.471095
## iter  11 value -0.471095
## iter  12 value -0.471096
## iter  13 value -0.471096
## iter  14 value -0.471096
## iter  15 value -0.471097
## iter  16 value -0.471097
## iter  16 value -0.471097
## iter  16 value -0.471097
## final  value -0.471097 
## converged
## initial  value -0.473585 
## iter   2 value -0.473664
## iter   3 value -0.473721
## iter   4 value -0.473823
## iter   5 value -0.473871
## iter   6 value -0.473885
## iter   7 value -0.473886
## iter   8 value -0.473886
## iter   8 value -0.473886
## iter   8 value -0.473886
## final  value -0.473886 
## converged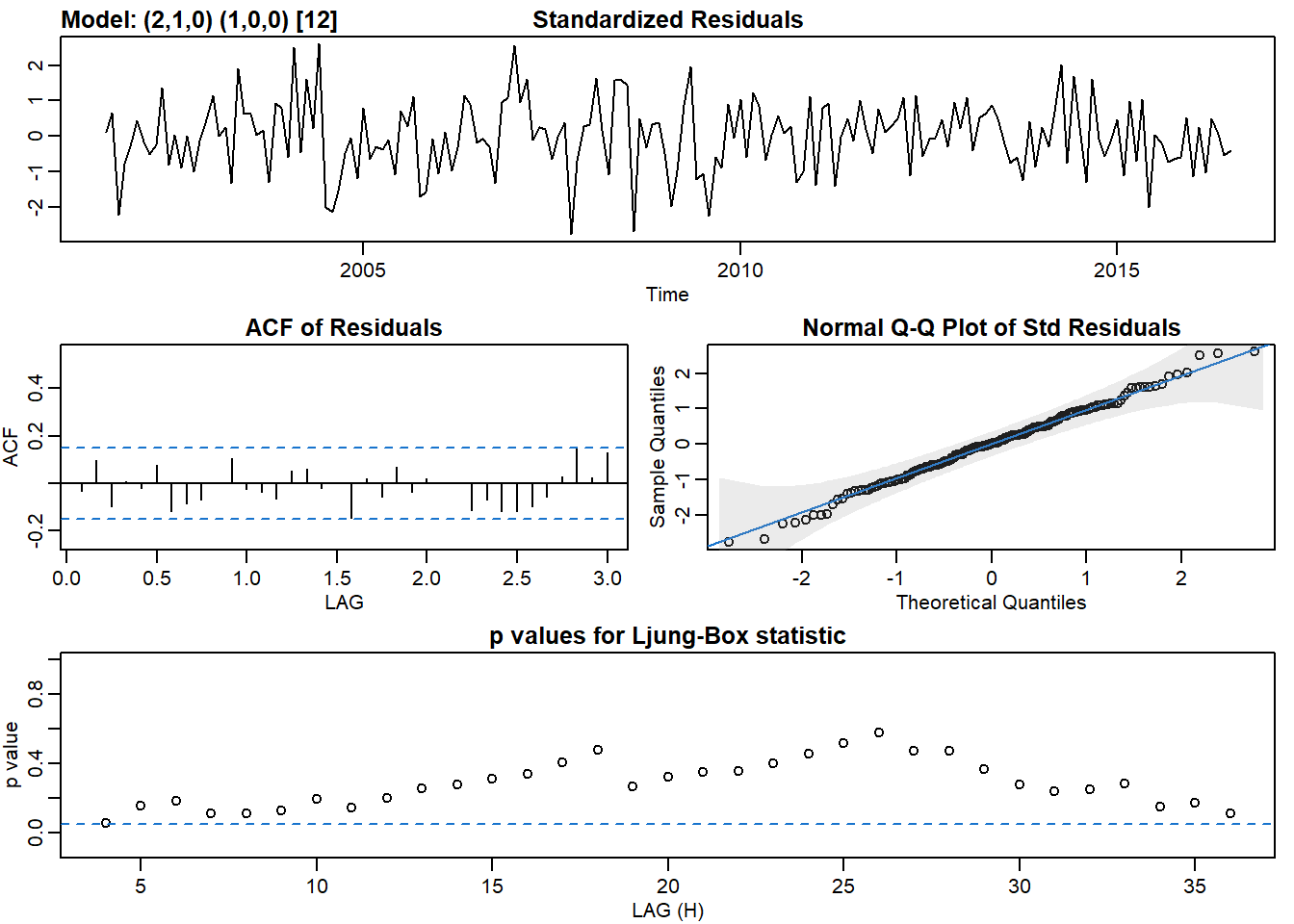

## $fit
## 
## Call:
## stats::arima(x = xdata, order = c(p, d, q), seasonal = list(order = c(P, D, 
##     Q), period = S), xreg = constant, transform.pars = trans, fixed = fixed, 
##     optim.control = list(trace = trc, REPORT = 1, reltol = tol))
## 
## Coefficients:
##          ar1      ar2    sar1  constant
##       0.9154  -0.2494  0.3237    0.2353
## s.e.  0.0733   0.0739  0.0715    0.1973
## 
## sigma^2 estimated as 0.3828:  log likelihood = -169.16,  aic = 348.33
## 
## $degrees_of_freedom
## [1] 175
## 
## $ttable
##          Estimate     SE t.value p.value
## ar1        0.9154 0.0733 12.4955  0.0000
## ar2       -0.2494 0.0739 -3.3728  0.0009
## sar1       0.3237 0.0715  4.5238  0.0000
## constant   0.2353 0.1973  1.1923  0.2347
## 
## $AIC
## [1] 1.945971
## 
## $AICc
## [1] 1.947256
## 
## $BIC
## [1] 2.035005

6.4 Unemployment

plot(unemp)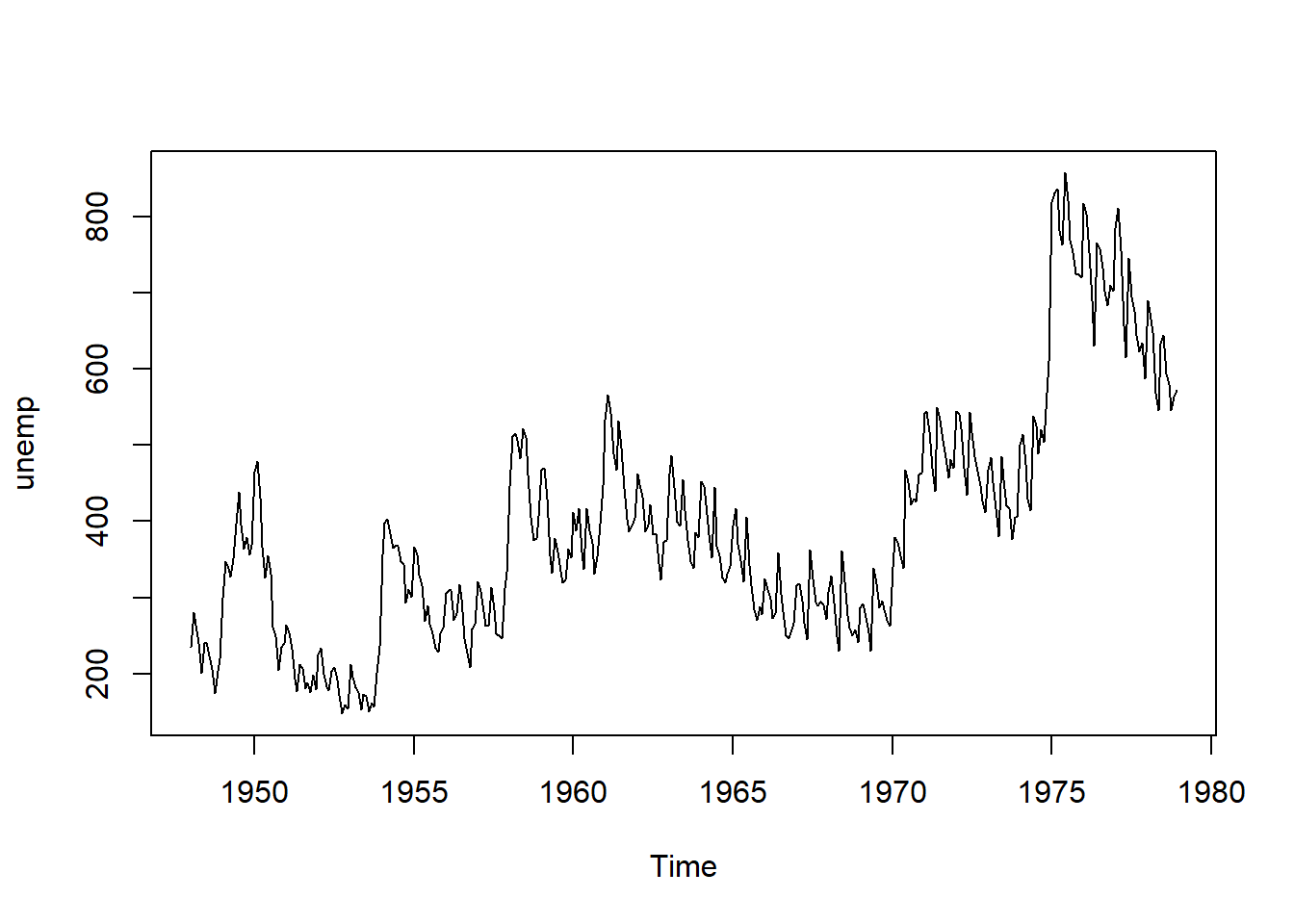

d_unemp <- diff(unemp)

plot(d_unemp)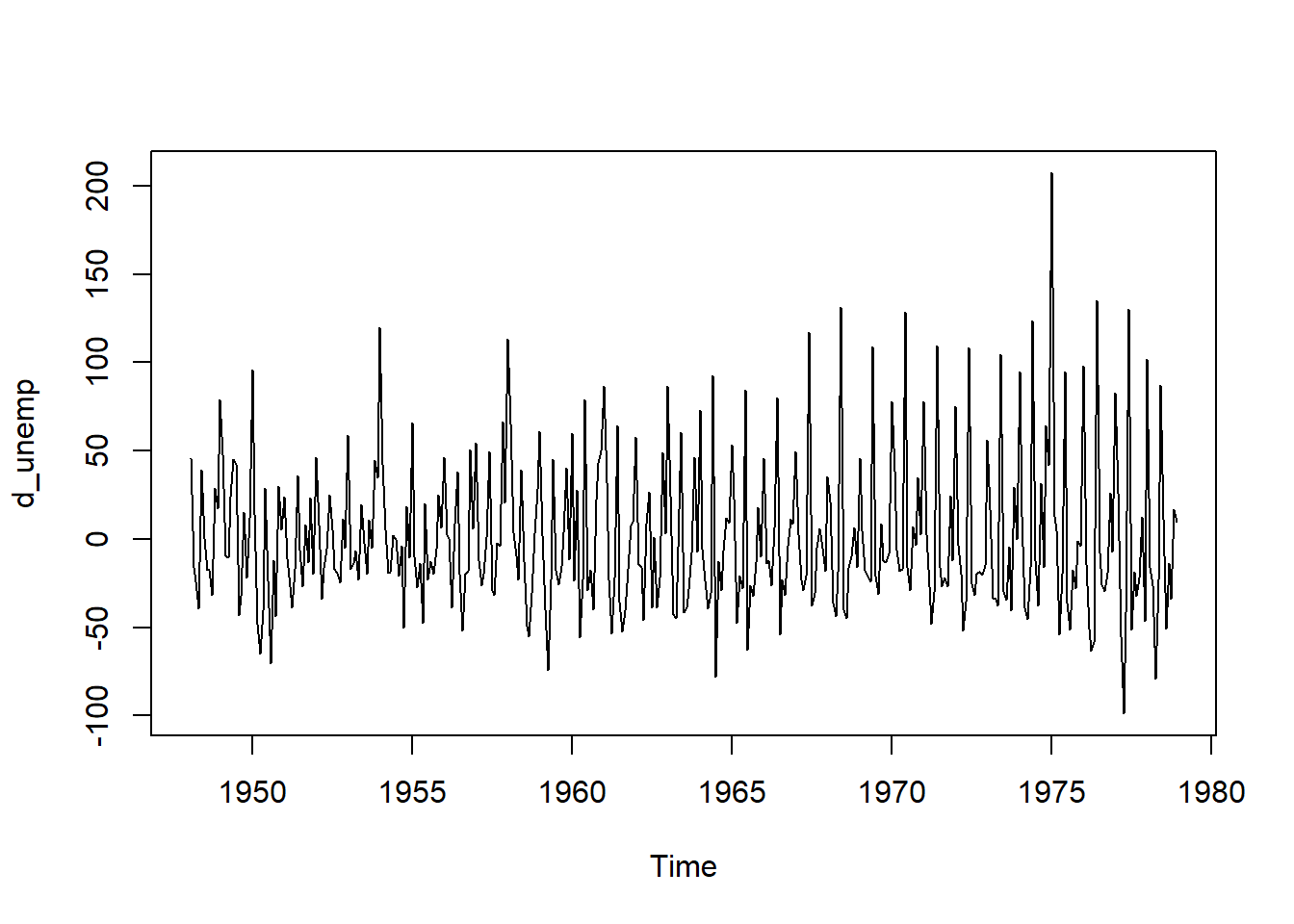

# Plot seasonal differenced diff_unemp
dd_unemp <- diff(d_unemp, lag = 12)   
plot(dd_unemp)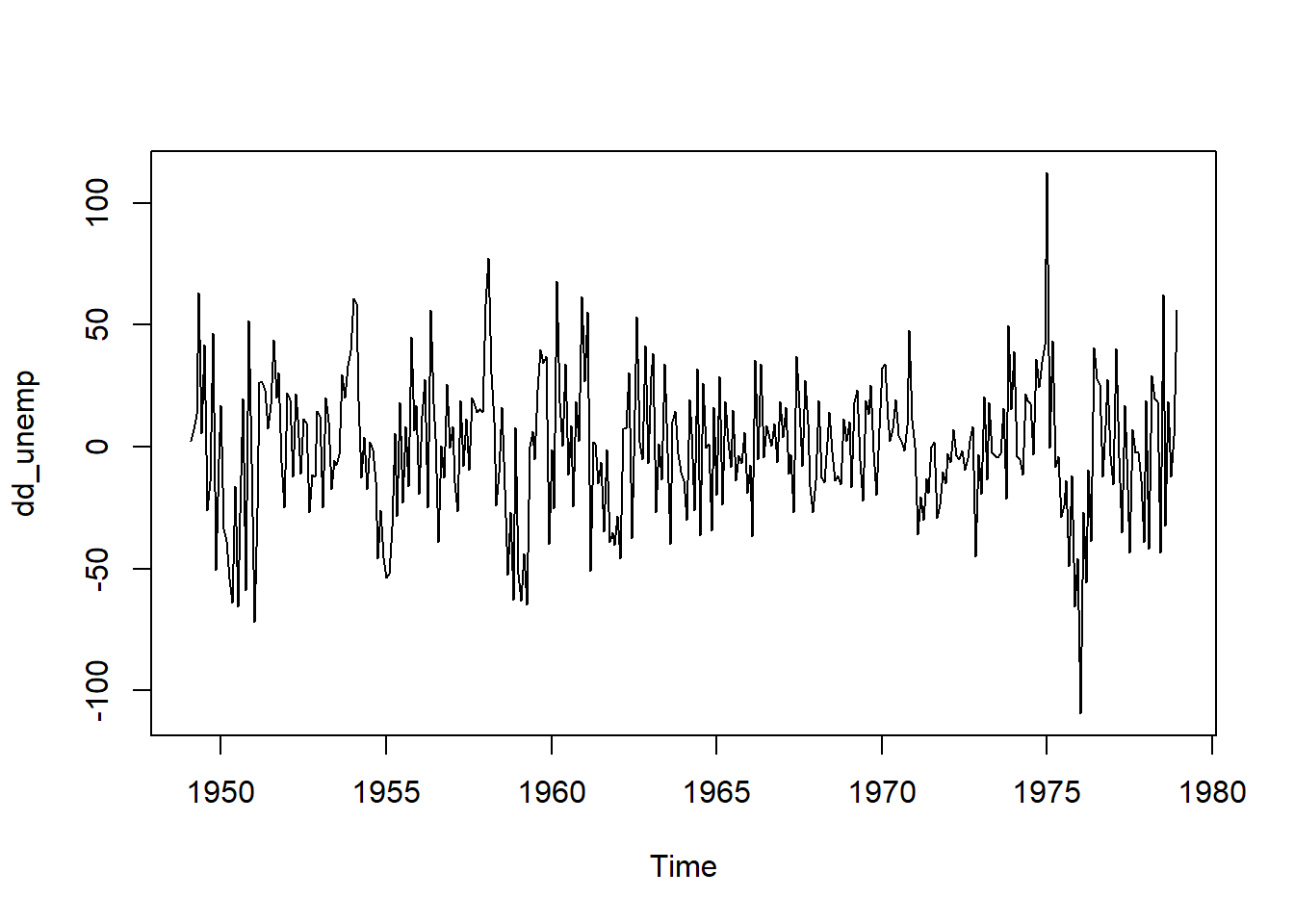

# Plot P/ACF pair of the fully differenced data to lag 60
dd_unemp <- diff(diff(unemp), lag = 12)
acf2(dd_unemp, max.lag = 60)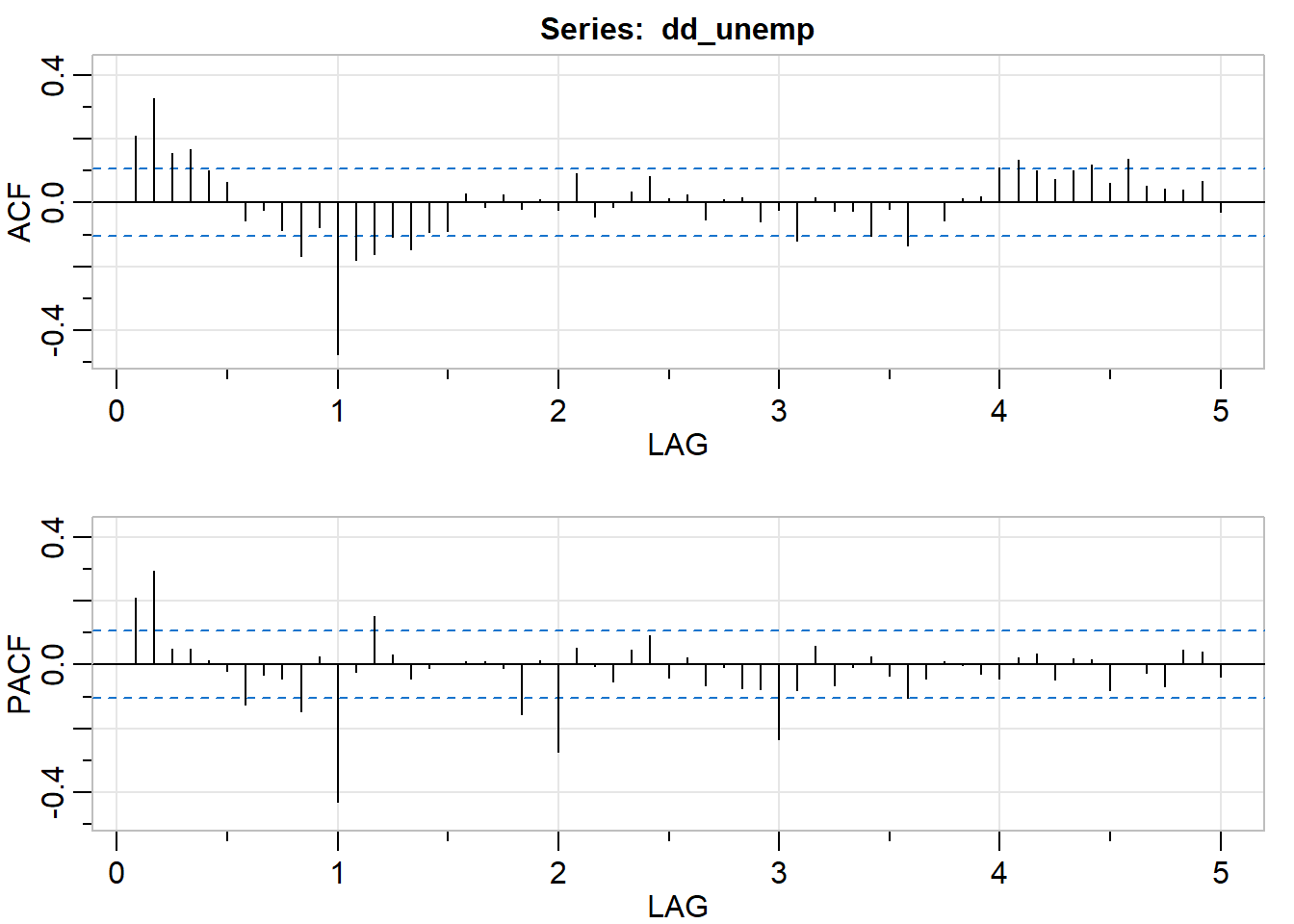

##      [,1] [,2] [,3] [,4] [,5]  [,6]  [,7]  [,8]  [,9] [,10] [,11] [,12] [,13]
## ACF  0.21 0.33 0.15 0.17 0.10  0.06 -0.06 -0.02 -0.09 -0.17 -0.08 -0.48 -0.18
## PACF 0.21 0.29 0.05 0.05 0.01 -0.02 -0.12 -0.03 -0.05 -0.15  0.02 -0.43 -0.02
##      [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
## ACF  -0.16 -0.11 -0.15 -0.09 -0.09  0.03 -0.01  0.02 -0.02  0.01 -0.02  0.09
## PACF  0.15  0.03 -0.04 -0.01  0.00  0.01  0.01 -0.01 -0.16  0.01 -0.27  0.05
##      [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37]
## ACF  -0.05 -0.01  0.03  0.08  0.01  0.03 -0.05  0.01  0.02 -0.06 -0.02 -0.12
## PACF -0.01 -0.05  0.05  0.09 -0.04  0.02 -0.07 -0.01 -0.08 -0.08 -0.23 -0.08
##      [,38] [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48] [,49]
## ACF   0.01 -0.03 -0.03 -0.10 -0.02 -0.13  0.00 -0.06  0.01  0.02  0.11  0.13
## PACF  0.06 -0.07 -0.01  0.03 -0.03 -0.11 -0.04  0.01  0.00 -0.03 -0.04  0.02
##      [,50] [,51] [,52] [,53] [,54] [,55] [,56] [,57] [,58] [,59] [,60]
## ACF   0.10  0.07  0.10  0.12  0.06  0.14  0.05  0.04  0.04  0.07 -0.03
## PACF  0.03 -0.05  0.02  0.02 -0.08  0.00 -0.03 -0.07  0.05  0.04 -0.04

# Fit an appropriate model
sarima(unemp, p = 2, d = 1, q = 0, P = 0, D = 1, Q = 1, S = 12)

## initial  value 3.340809 
## iter   2 value 3.105512
## iter   3 value 3.086631
## iter   4 value 3.079778
## iter   5 value 3.069447
## iter   6 value 3.067659
## iter   7 value 3.067426
## iter   8 value 3.067418
## iter   8 value 3.067418
## final  value 3.067418 
## converged
## initial  value 3.065481 
## iter   2 value 3.065478
## iter   3 value 3.065477
## iter   3 value 3.065477
## iter   3 value 3.065477
## final  value 3.065477 
## converged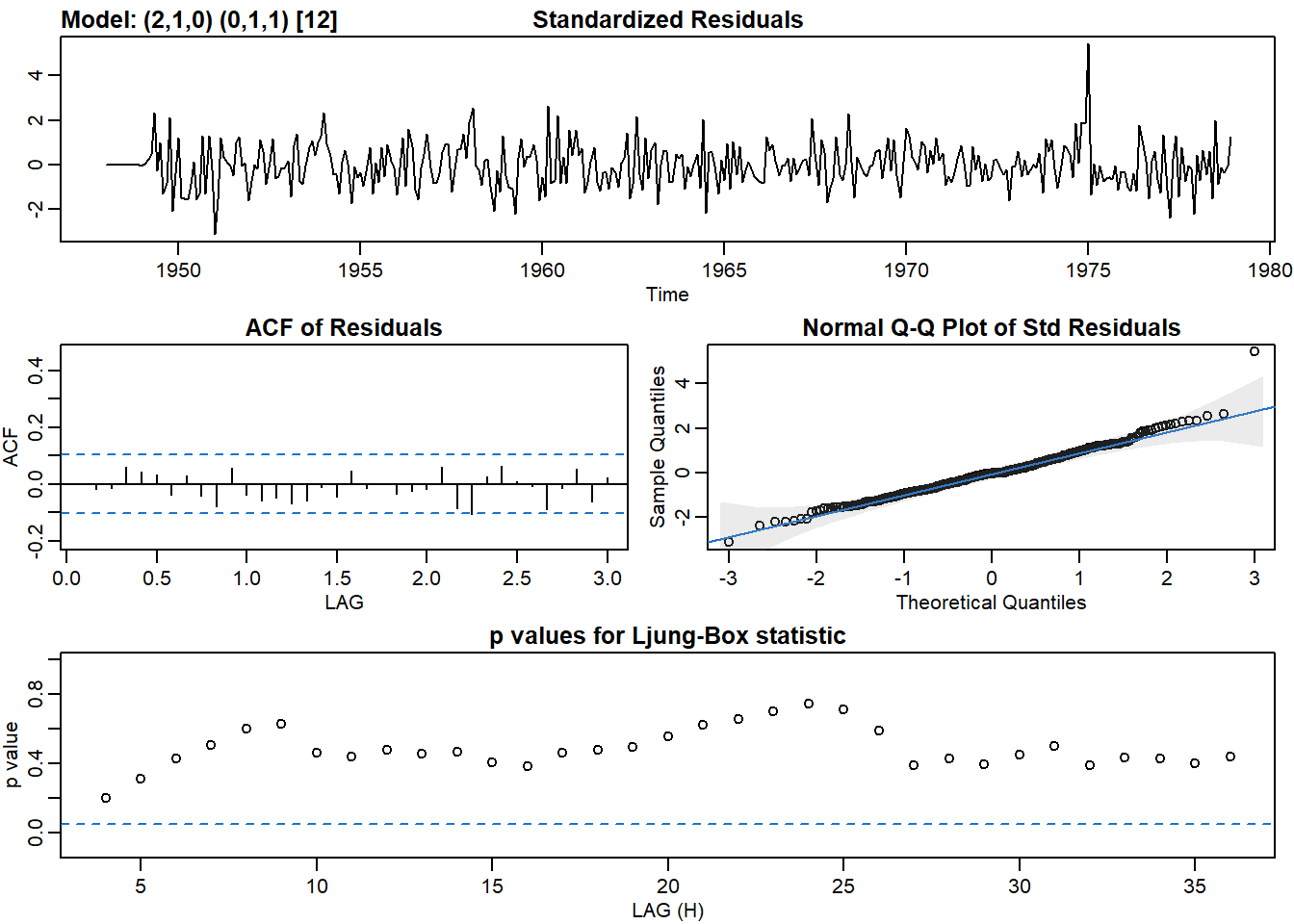

## $fit
## 
## Call:
## stats::arima(x = xdata, order = c(p, d, q), seasonal = list(order = c(P, D, 
##     Q), period = S), include.mean = !no.constant, transform.pars = trans, fixed = fixed, 
##     optim.control = list(trace = trc, REPORT = 1, reltol = tol))
## 
## Coefficients:
##          ar1     ar2     sma1
##       0.1351  0.2464  -0.6953
## s.e.  0.0513  0.0515   0.0381
## 
## sigma^2 estimated as 449.6:  log likelihood = -1609.91,  aic = 3227.81
## 
## $degrees_of_freedom
## [1] 356
## 
## $ttable
##      Estimate     SE  t.value p.value
## ar1    0.1351 0.0513   2.6326  0.0088
## ar2    0.2464 0.0515   4.7795  0.0000
## sma1  -0.6953 0.0381 -18.2362  0.0000
## 
## $AIC
## [1] 8.723811
## 
## $AICc
## [1] 8.723988
## 
## $BIC
## [1] 8.765793