10 Chapter 5 Lab
10.1 Oil Return
An example using ARMA(1,1) process:
library(astsa)
plot(oil)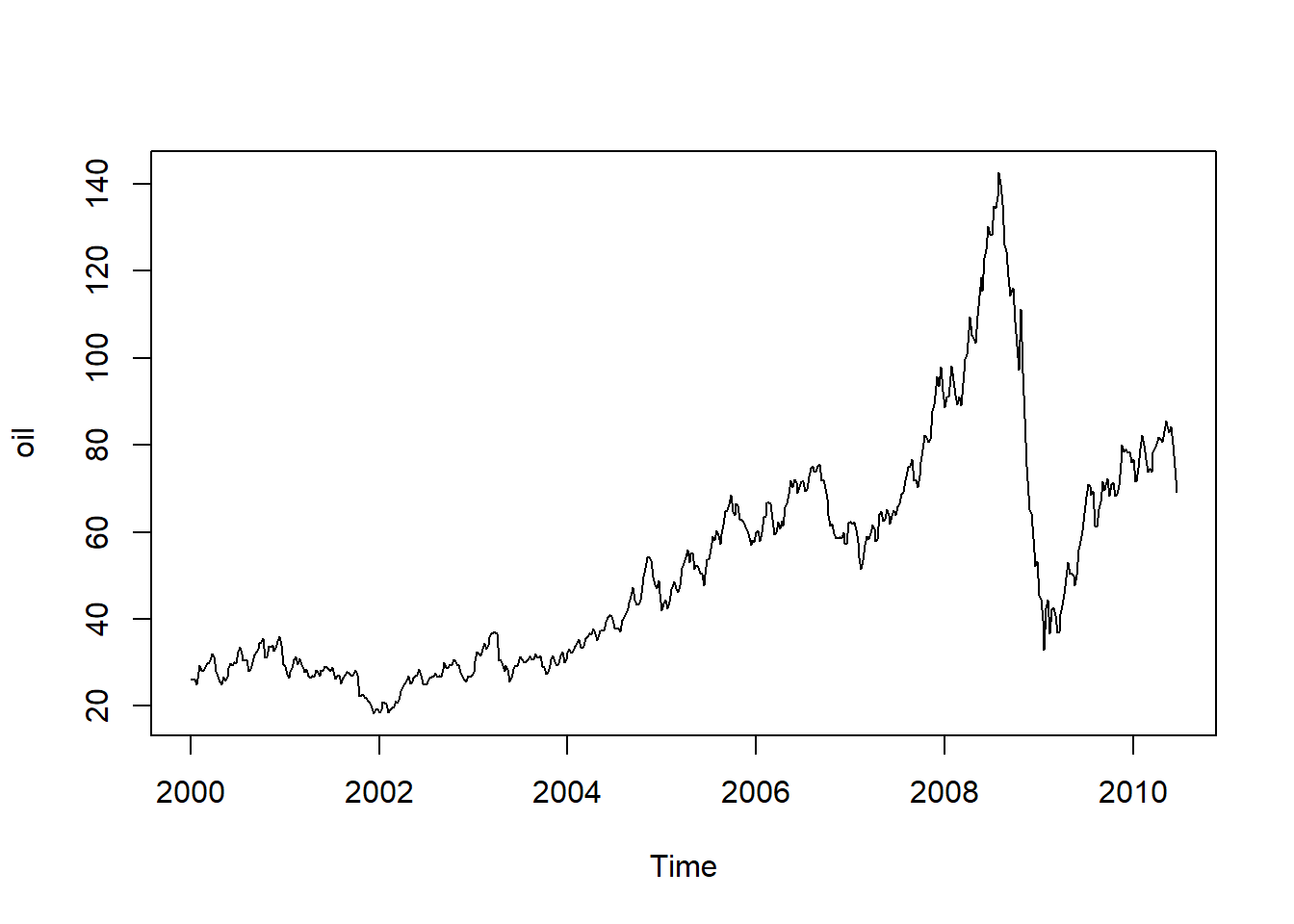
# Calculate approximate oil returns
oil_returns <- diff(log(oil))
# Plot oil_returns. Notice the outliers.
plot(oil_returns)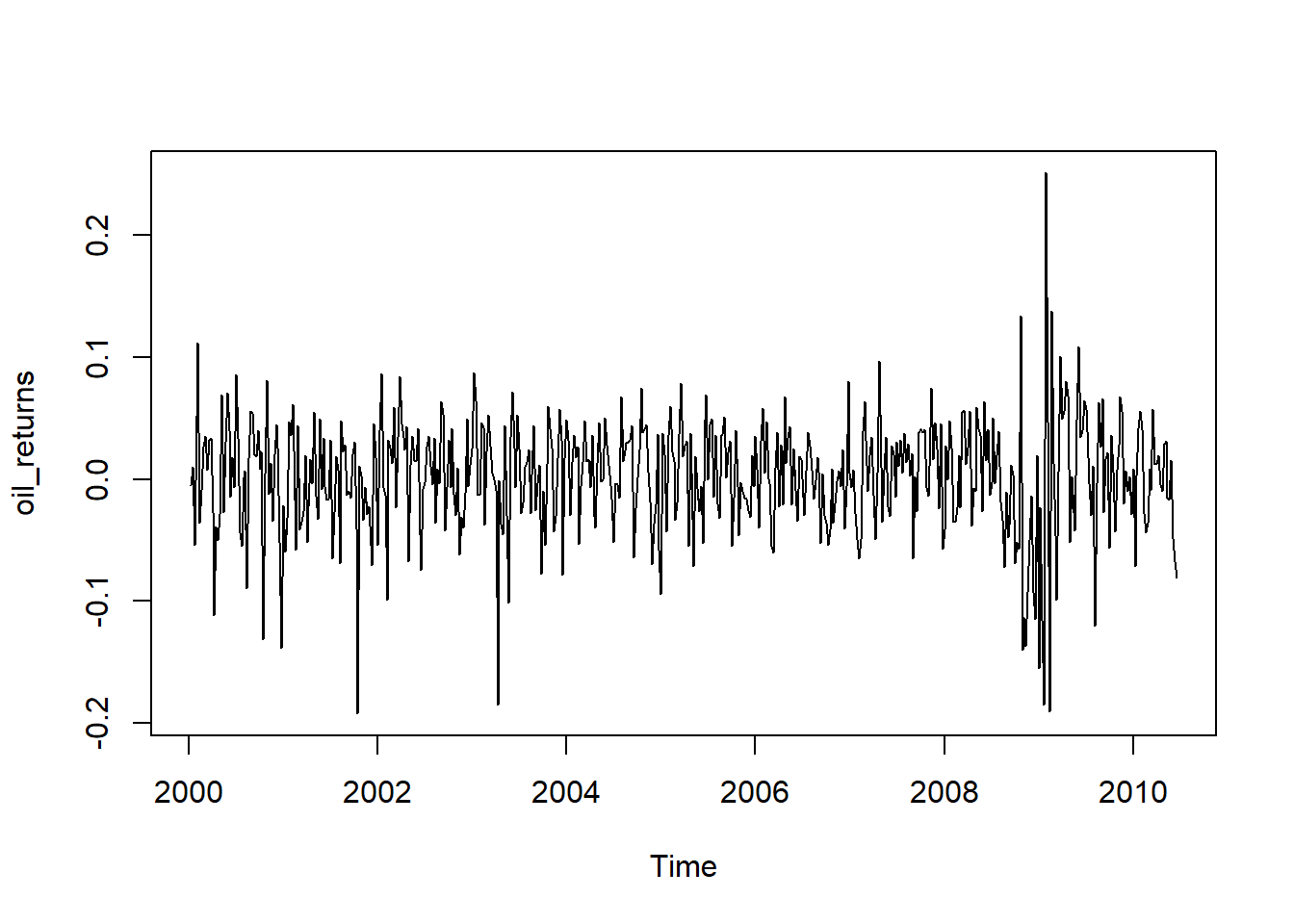
# Plot the P/ACF pair for oil_returns
acf2(oil_returns)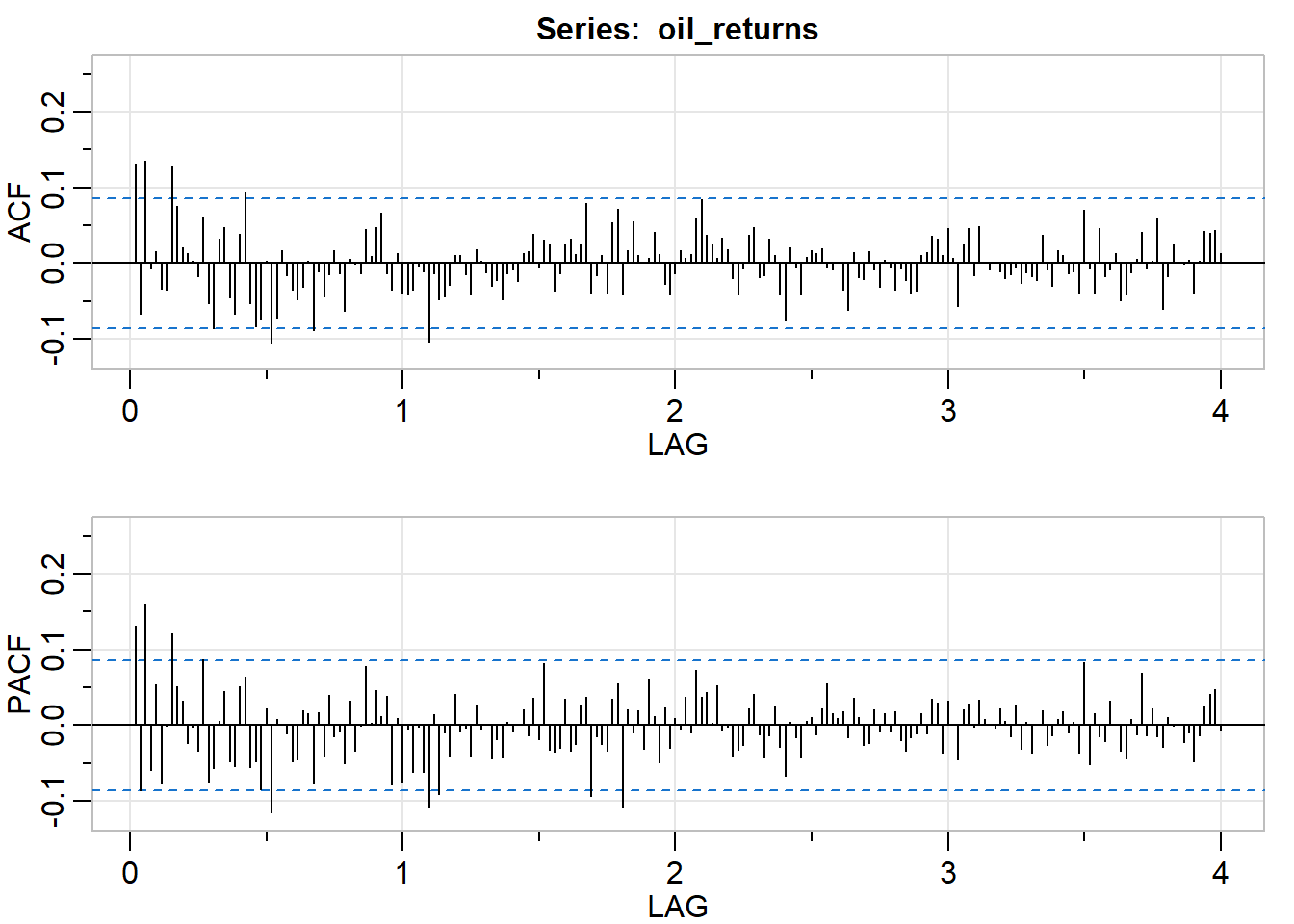
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
## ACF 0.13 -0.07 0.13 -0.01 0.02 -0.03 -0.03 0.13 0.08 0.02 0.01 0 -0.02
## PACF 0.13 -0.09 0.16 -0.06 0.05 -0.08 0.00 0.12 0.05 0.03 -0.02 0 -0.03
## [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
## ACF 0.06 -0.05 -0.09 0.03 0.05 -0.05 -0.07 0.04 0.09 -0.05 -0.08 -0.07
## PACF 0.09 -0.07 -0.06 0.01 0.04 -0.05 -0.05 0.05 0.06 -0.06 -0.05 -0.08
## [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37]
## ACF 0.00 -0.11 -0.07 0.02 -0.02 -0.03 -0.05 -0.03 0.00 -0.09 -0.01 -0.04
## PACF 0.02 -0.11 0.01 0.00 -0.01 -0.05 -0.04 0.02 0.02 -0.08 0.02 -0.04
## [,38] [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48] [,49]
## ACF -0.01 0.02 -0.01 -0.06 0.01 0.00 -0.01 0.04 0.01 0.05 0.07 -0.01
## PACF 0.04 -0.01 -0.01 -0.05 0.03 -0.03 0.00 0.08 0.00 0.05 0.01 0.04
## [,50] [,51] [,52] [,53] [,54] [,55] [,56] [,57] [,58] [,59] [,60] [,61]
## ACF -0.03 0.01 -0.04 -0.04 -0.03 0 -0.01 -0.10 -0.01 -0.05 -0.04 -0.03
## PACF -0.08 0.01 -0.07 0.00 -0.06 0 -0.06 -0.11 0.01 -0.09 -0.01 -0.04
## [,62] [,63] [,64] [,65] [,66] [,67] [,68] [,69] [,70] [,71] [,72] [,73]
## ACF 0.01 0.01 -0.01 -0.04 0.02 0 -0.01 -0.03 -0.02 -0.05 -0.01 -0.01
## PACF 0.04 -0.01 0.00 -0.04 0.03 0 0.00 -0.04 -0.02 -0.04 0.00 -0.01
## [,74] [,75] [,76] [,77] [,78] [,79] [,80] [,81] [,82] [,83] [,84] [,85]
## ACF -0.02 0.01 0.02 0.04 -0.01 0.03 0.02 -0.04 -0.01 0.02 0.03 0.01
## PACF 0.00 0.02 -0.01 0.04 -0.02 0.08 -0.03 -0.03 -0.03 0.03 -0.03 -0.02
## [,86] [,87] [,88] [,89] [,90] [,91] [,92] [,93] [,94] [,95] [,96] [,97]
## ACF 0.03 0.08 -0.04 -0.02 0.01 -0.04 0.05 0.07 -0.04 0.02 0.05 0.01
## PACF 0.03 0.04 -0.09 -0.01 -0.02 -0.03 0.03 0.05 -0.11 0.02 -0.01 0.02
## [,98] [,99] [,100] [,101] [,102] [,103] [,104] [,105] [,106] [,107] [,108]
## ACF 0.00 0.01 0.04 0.01 -0.03 -0.04 -0.01 0.02 0.01 0.01 0.06
## PACF -0.03 0.06 0.01 -0.05 0.02 -0.03 0.01 0.00 0.04 -0.01 0.07
## [,109] [,110] [,111] [,112] [,113] [,114] [,115] [,116] [,117] [,118]
## ACF 0.08 0.04 0.02 0.01 0.03 0.02 -0.02 -0.04 -0.01 0.04
## PACF 0.04 0.04 0.00 0.05 -0.01 0.00 -0.04 -0.03 -0.03 0.02
## [,119] [,120] [,121] [,122] [,123] [,124] [,125] [,126] [,127] [,128]
## ACF 0.05 -0.02 -0.02 0.03 0.01 -0.04 -0.08 0.02 0.00 -0.04
## PACF 0.04 -0.01 -0.04 -0.01 0.03 -0.03 -0.07 0.00 -0.02 -0.04
## [,129] [,130] [,131] [,132] [,133] [,134] [,135] [,136] [,137] [,138]
## ACF 0.01 0.02 0.01 0.02 0.00 -0.01 0.00 -0.03 -0.06 0.01
## PACF 0.01 0.01 -0.01 0.02 0.05 0.02 0.01 0.02 -0.02 0.04
## [,139] [,140] [,141] [,142] [,143] [,144] [,145] [,146] [,147] [,148]
## ACF -0.02 -0.02 0.02 -0.01 -0.03 0.00 0.00 -0.04 -0.01 -0.02
## PACF 0.01 -0.03 -0.02 0.02 -0.01 0.02 -0.01 0.02 -0.02 -0.03
## [,149] [,150] [,151] [,152] [,153] [,154] [,155] [,156] [,157] [,158]
## ACF -0.04 -0.04 0.01 0.01 0.04 0.03 0.01 0.05 0.01 -0.06
## PACF -0.02 -0.01 0.02 -0.01 0.04 0.03 -0.04 0.03 0.00 -0.05
## [,159] [,160] [,161] [,162] [,163] [,164] [,165] [,166] [,167] [,168]
## ACF 0.02 0.05 -0.02 0.05 0.00 -0.01 0 -0.01 -0.02 -0.01
## PACF 0.02 0.03 0.00 0.03 0.01 0.00 0 0.02 0.01 -0.01
## [,169] [,170] [,171] [,172] [,173] [,174] [,175] [,176] [,177] [,178]
## ACF 0.00 -0.03 -0.01 -0.02 -0.02 0.04 -0.01 -0.03 0.02 0.01
## PACF 0.03 -0.03 0.00 -0.04 0.00 0.02 -0.03 -0.01 0.01 0.02
## [,179] [,180] [,181] [,182] [,183] [,184] [,185] [,186] [,187] [,188]
## ACF -0.01 -0.01 -0.04 0.07 -0.01 -0.04 0.05 -0.02 -0.01 0.01
## PACF -0.01 0.00 -0.04 0.08 -0.05 0.02 -0.01 -0.02 0.03 0.00
## [,189] [,190] [,191] [,192] [,193] [,194] [,195] [,196] [,197] [,198]
## ACF -0.05 -0.04 -0.01 0.01 0.04 -0.01 0.00 0.06 -0.06 -0.02
## PACF -0.03 -0.04 0.01 -0.01 0.07 -0.01 0.02 -0.01 -0.03 0.01
## [,199] [,200] [,201] [,202] [,203] [,204] [,205] [,206] [,207] [,208]
## ACF 0.02 0 0.00 0.00 -0.04 0.00 0.04 0.04 0.04 0.01
## PACF 0.00 0 -0.02 -0.01 -0.05 -0.01 0.02 0.04 0.05 -0.01# Assuming both P/ACF are tailing, fit a model
sarima(oil_returns, p = 1, d = 0, q = 1)## initial value -3.057594
## iter 2 value -3.061420
## iter 3 value -3.067360
## iter 4 value -3.067479
## iter 5 value -3.071834
## iter 6 value -3.074359
## iter 7 value -3.074843
## iter 8 value -3.076656
## iter 9 value -3.080467
## iter 10 value -3.081546
## iter 11 value -3.081603
## iter 12 value -3.081615
## iter 13 value -3.081642
## iter 14 value -3.081643
## iter 14 value -3.081643
## iter 14 value -3.081643
## final value -3.081643
## converged
## initial value -3.082345
## iter 2 value -3.082345
## iter 3 value -3.082346
## iter 4 value -3.082346
## iter 5 value -3.082346
## iter 5 value -3.082346
## iter 5 value -3.082346
## final value -3.082346
## converged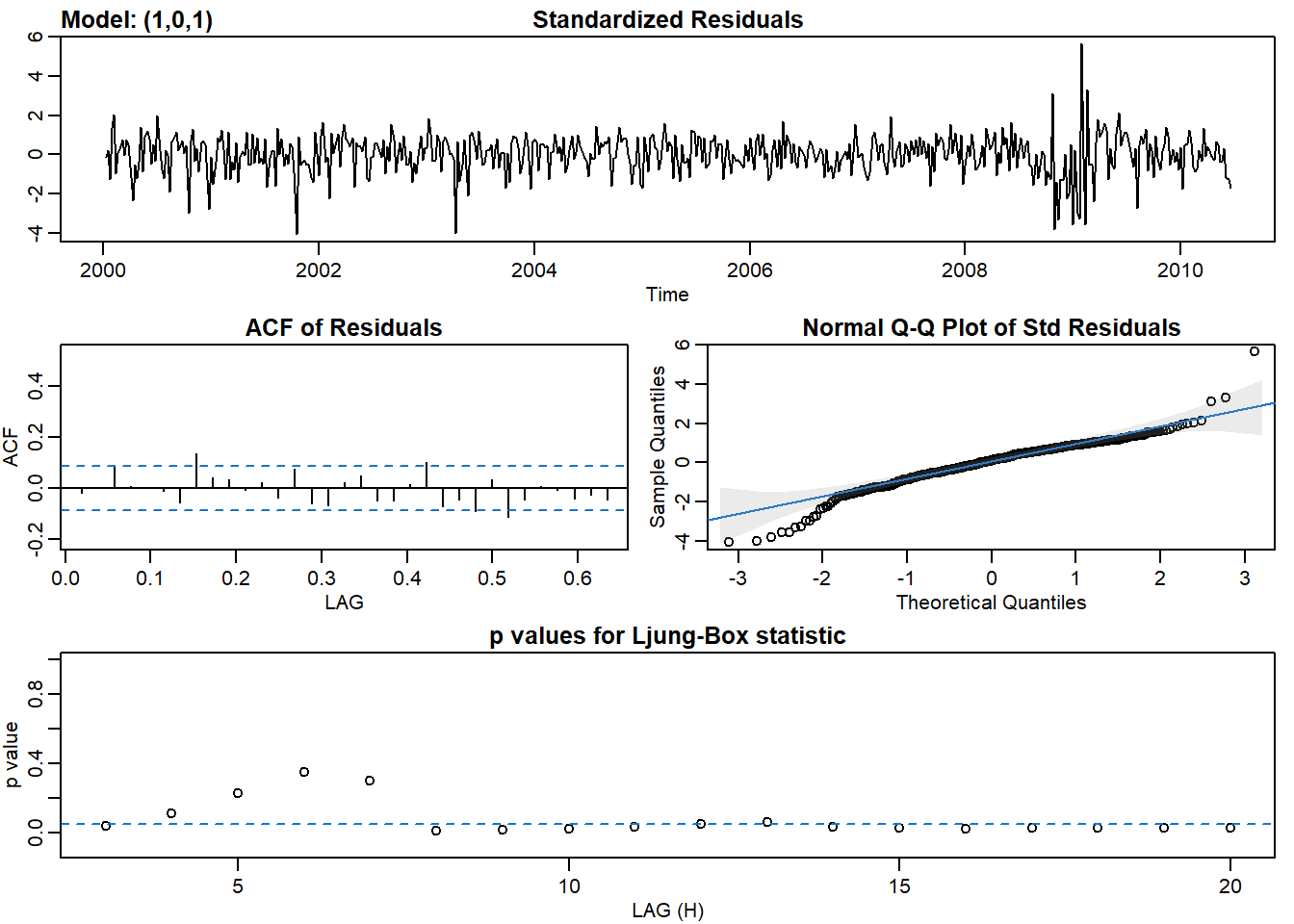
## $fit
##
## Call:
## stats::arima(x = xdata, order = c(p, d, q), seasonal = list(order = c(P, D,
## Q), period = S), xreg = xmean, include.mean = FALSE, transform.pars = trans,
## fixed = fixed, optim.control = list(trace = trc, REPORT = 1, reltol = tol))
##
## Coefficients:
## ar1 ma1 xmean
## -0.5264 0.7146 0.0018
## s.e. 0.0871 0.0683 0.0022
##
## sigma^2 estimated as 0.002102: log likelihood = 904.89, aic = -1801.79
##
## $degrees_of_freedom
## [1] 541
##
## $ttable
## Estimate SE t.value p.value
## ar1 -0.5264 0.0871 -6.0422 0.0000
## ma1 0.7146 0.0683 10.4699 0.0000
## xmean 0.0018 0.0022 0.7981 0.4252
##
## $AIC
## [1] -3.312109
##
## $AICc
## [1] -3.312027
##
## $BIC
## [1] -3.280499Oil price is hard to model since there is a 2008 peak period for oil price followed by a sharp drop due to the financial crisis. Taking the first order difference yields the daily return of oil, but the data is not quite stationary. The ACF and PACF suggests an ARMA(1,1) model, which I fitted to the differenced series. The residuals does not look like white noise and failed the Q-Q plot and Ljung-Box statistic.
10.2 Air Passengers
# Load data
library(astsa)
plot(AirPassengers)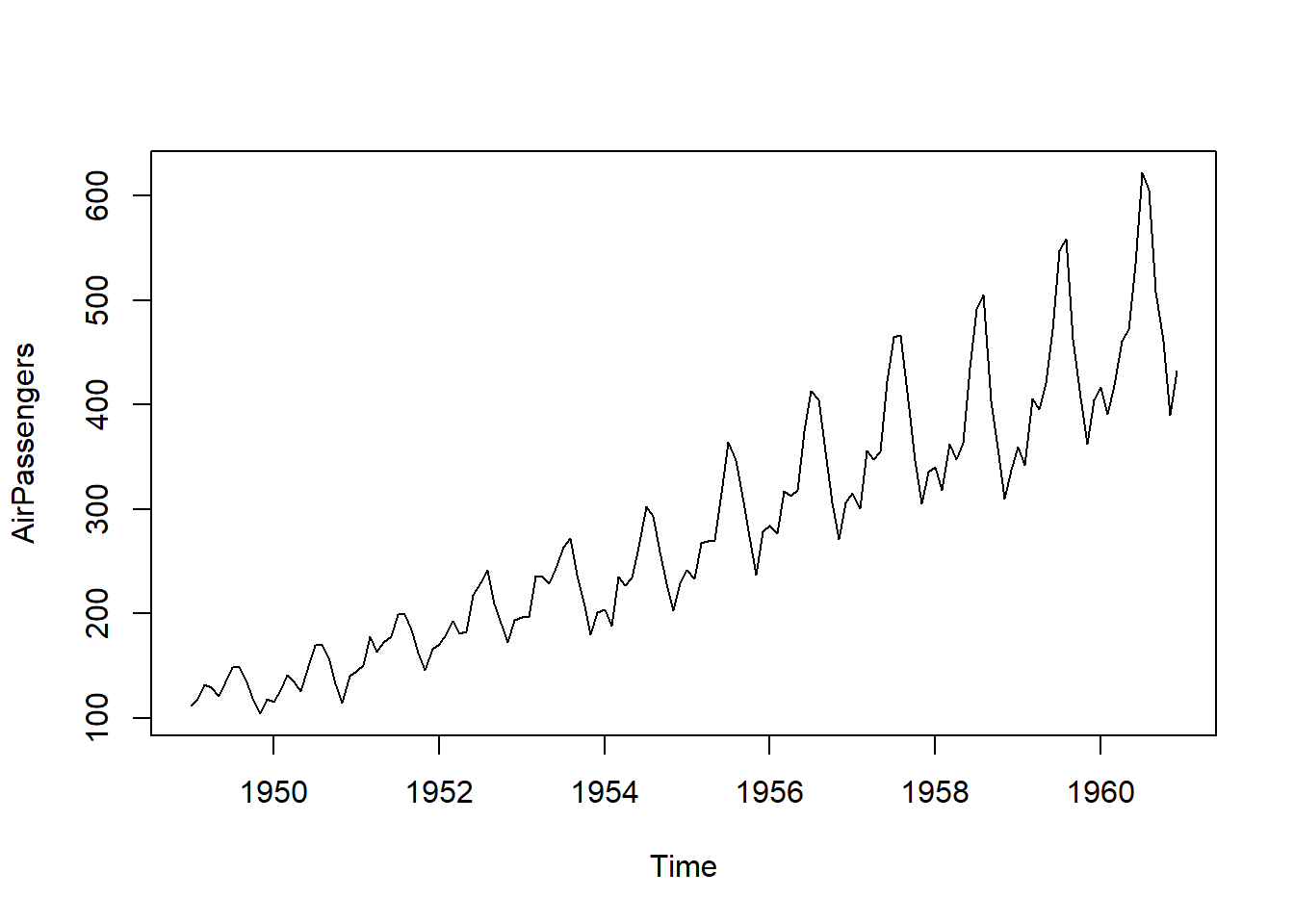
From the plot of Air Passengers, there are: trend, seasonal variation, heteroscedasticity (variance increases over time).
10.3 Birth Rate
plot(birth)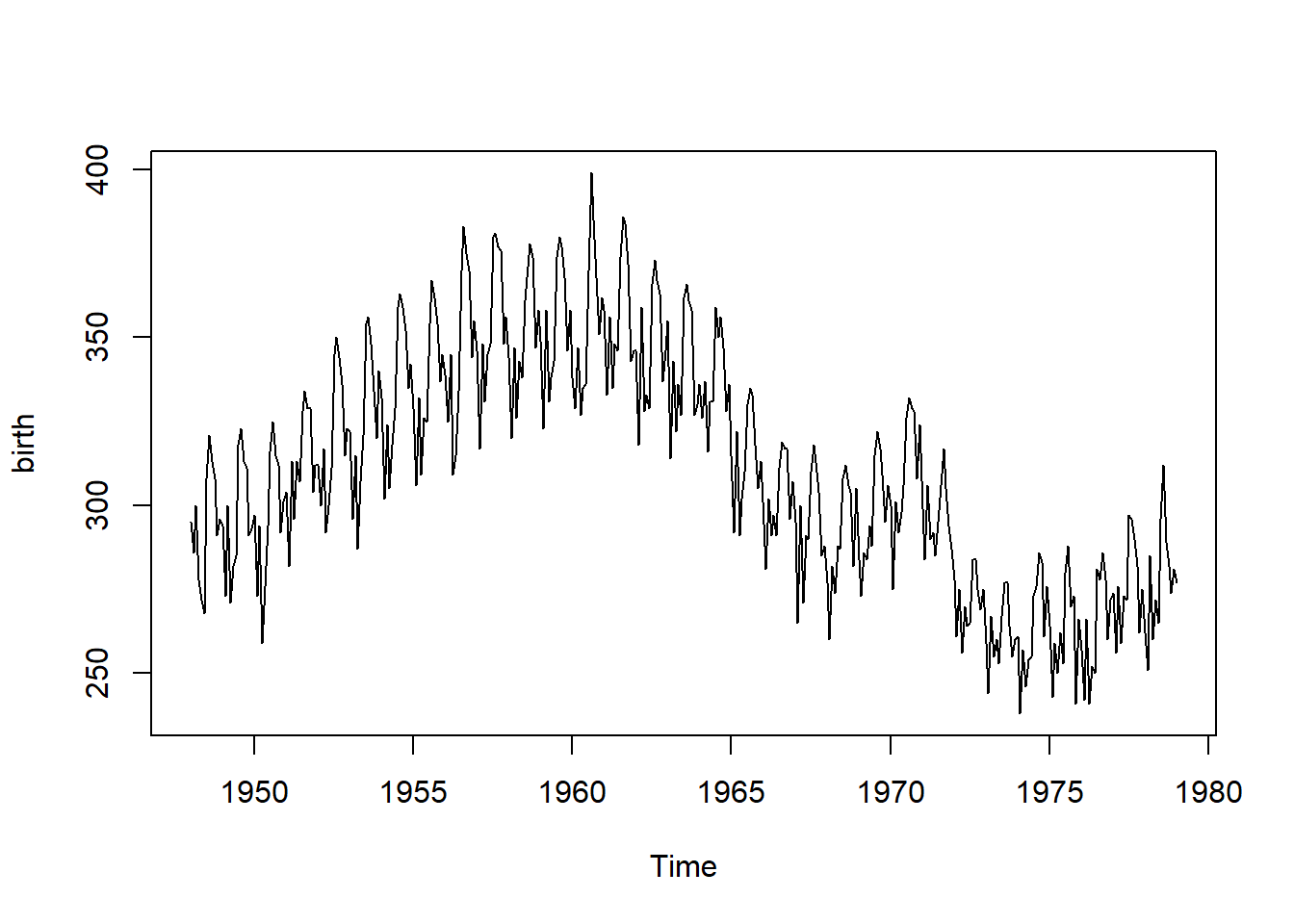
# Plot P/ACF to lag 60 of differenced data
d_birth <- diff(birth)
acf2(d_birth, max.lag = 60)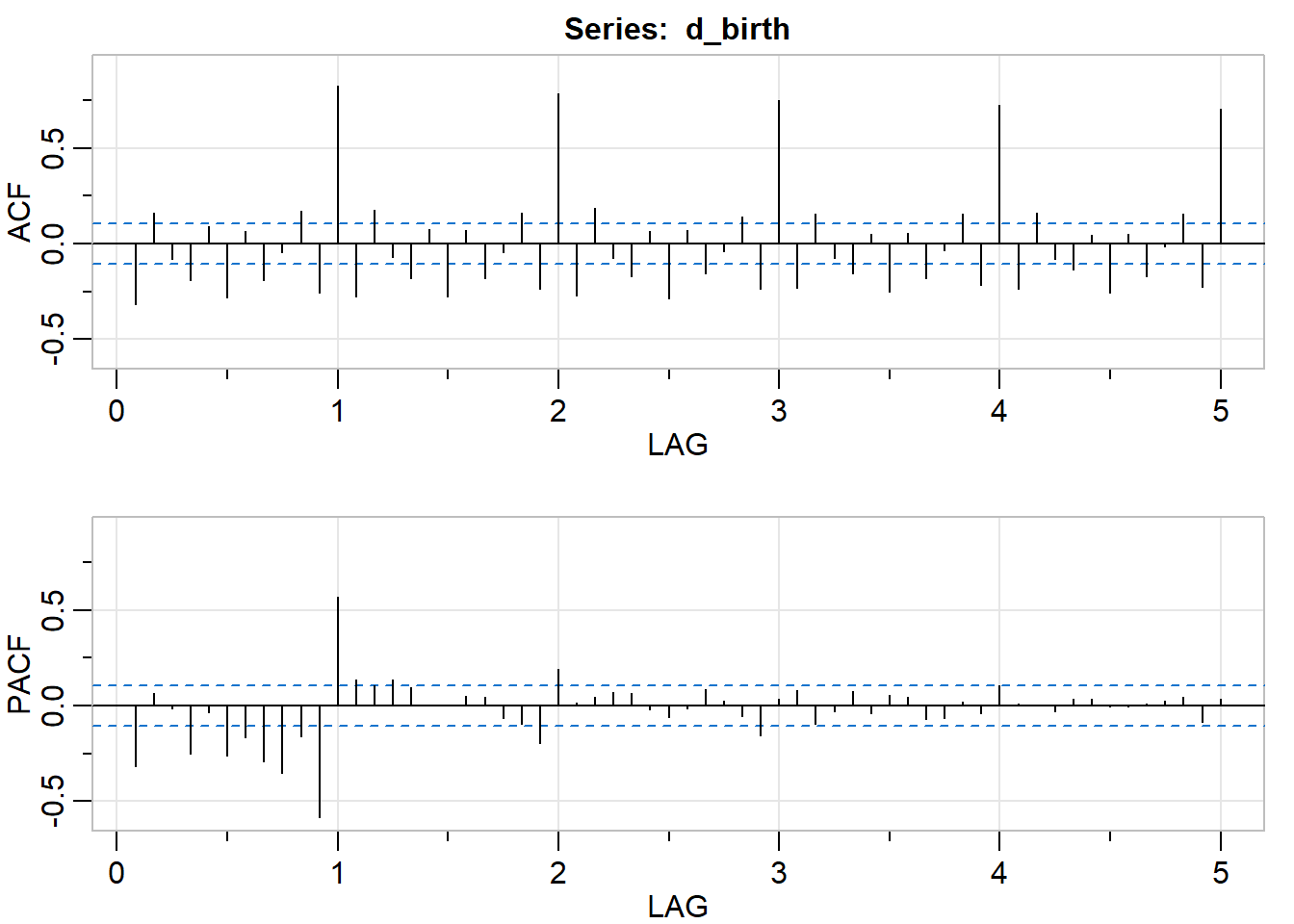
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
## ACF -0.32 0.16 -0.08 -0.19 0.09 -0.28 0.06 -0.19 -0.05 0.17 -0.26 0.82
## PACF -0.32 0.06 -0.01 -0.25 -0.03 -0.26 -0.17 -0.29 -0.35 -0.16 -0.59 0.57
## [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24]
## ACF -0.28 0.17 -0.07 -0.18 0.08 -0.28 0.07 -0.18 -0.05 0.16 -0.24 0.78
## PACF 0.13 0.11 0.13 0.09 0.00 0.00 0.05 0.04 -0.07 -0.10 -0.20 0.19
## [,25] [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36]
## ACF -0.27 0.19 -0.08 -0.17 0.07 -0.29 0.07 -0.15 -0.04 0.14 -0.24 0.75
## PACF 0.01 0.05 0.07 0.07 -0.02 -0.06 -0.02 0.09 0.03 -0.06 -0.16 0.03
## [,37] [,38] [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48]
## ACF -0.23 0.16 -0.08 -0.15 0.05 -0.25 0.06 -0.18 -0.03 0.15 -0.22 0.72
## PACF 0.08 -0.10 -0.03 0.07 -0.04 0.06 0.04 -0.07 -0.06 0.02 -0.04 0.10
## [,49] [,50] [,51] [,52] [,53] [,54] [,55] [,56] [,57] [,58] [,59] [,60]
## ACF -0.24 0.16 -0.08 -0.13 0.05 -0.26 0.05 -0.17 -0.02 0.15 -0.23 0.70
## PACF 0.01 0.00 -0.03 0.04 0.03 0.00 -0.01 0.01 0.03 0.04 -0.09 0.04# Plot P/ACF to lag 60 of seasonal differenced data
dd_birth <- diff(d_birth, lag = 12)
acf2(dd_birth, max.lag = 60)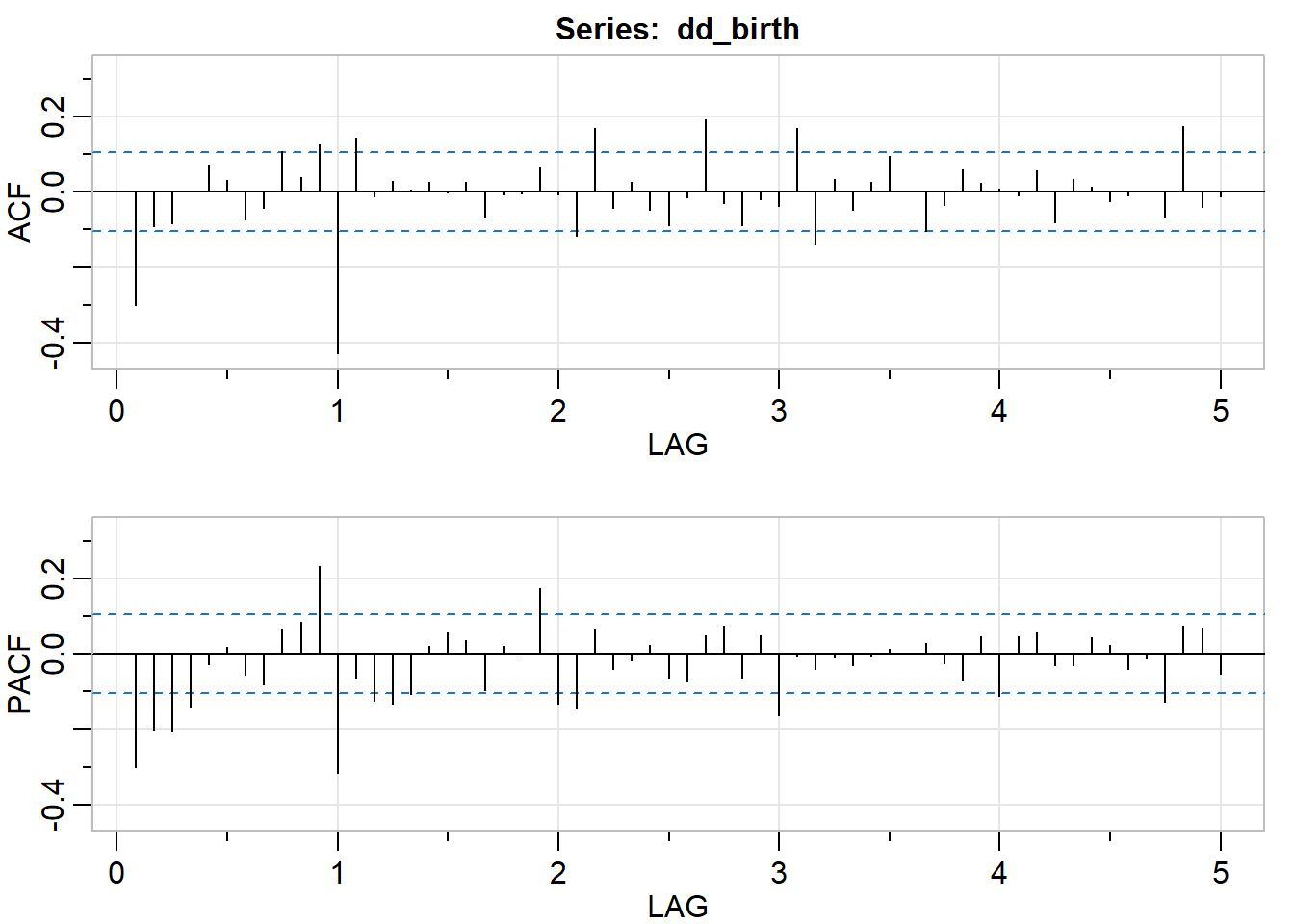
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
## ACF -0.3 -0.09 -0.09 0.00 0.07 0.03 -0.07 -0.04 0.11 0.04 0.13 -0.43 0.14
## PACF -0.3 -0.20 -0.21 -0.14 -0.03 0.02 -0.06 -0.08 0.06 0.08 0.23 -0.32 -0.06
## [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
## ACF -0.01 0.03 0.01 0.02 0.00 0.03 -0.07 -0.01 0 0.06 -0.01 -0.12
## PACF -0.13 -0.13 -0.11 0.02 0.06 0.04 -0.10 0.02 0 0.17 -0.13 -0.14
## [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37]
## ACF 0.17 -0.04 0.03 -0.05 -0.09 -0.01 0.19 -0.03 -0.09 -0.02 -0.04 0.17
## PACF 0.07 -0.04 -0.02 0.02 -0.06 -0.07 0.05 0.07 -0.06 0.05 -0.16 -0.01
## [,38] [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48] [,49]
## ACF -0.14 0.03 -0.05 0.03 0.10 0 -0.10 -0.03 0.06 0.02 0.01 -0.01
## PACF -0.04 -0.01 -0.03 -0.01 0.01 0 0.03 -0.02 -0.07 0.05 -0.11 0.05
## [,50] [,51] [,52] [,53] [,54] [,55] [,56] [,57] [,58] [,59] [,60]
## ACF 0.06 -0.08 0.03 0.01 -0.02 -0.01 0.00 -0.07 0.17 -0.04 -0.01
## PACF 0.06 -0.03 -0.03 0.04 0.02 -0.04 -0.01 -0.13 0.07 0.07 -0.05# Fit SARIMA(0,1,1)x(0,1,1)_12. What happens?
sarima(birth, p = 0, d = 1, q = 1, P = 0, D = 1, Q = 1, S = 12)## initial value 2.219164
## iter 2 value 2.013310
## iter 3 value 1.988107
## iter 4 value 1.980026
## iter 5 value 1.967594
## iter 6 value 1.965384
## iter 7 value 1.965049
## iter 8 value 1.964993
## iter 9 value 1.964992
## iter 9 value 1.964992
## iter 9 value 1.964992
## final value 1.964992
## converged
## initial value 1.951264
## iter 2 value 1.945867
## iter 3 value 1.945729
## iter 4 value 1.945723
## iter 5 value 1.945723
## iter 5 value 1.945723
## iter 5 value 1.945723
## final value 1.945723
## converged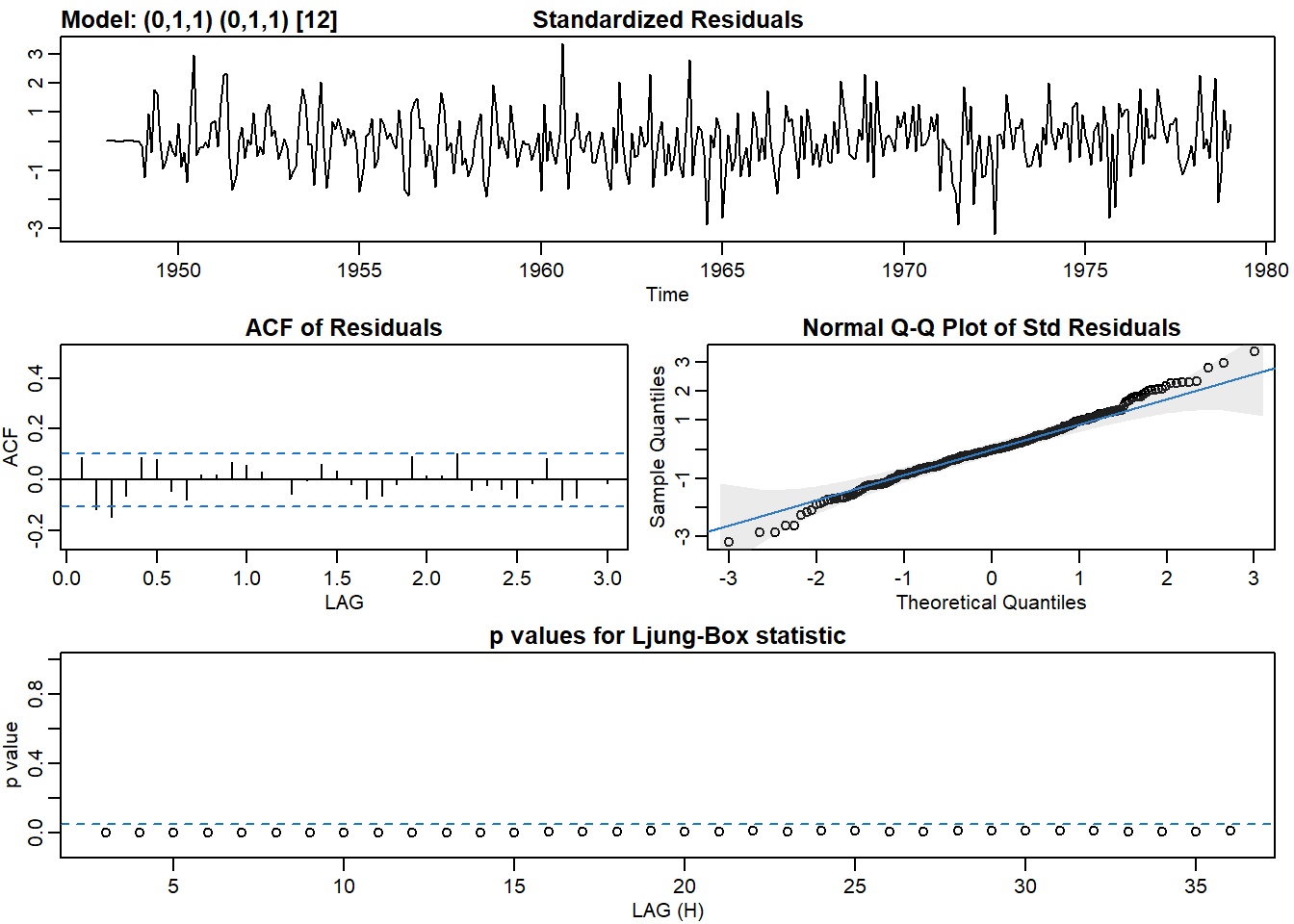
## $fit
##
## Call:
## stats::arima(x = xdata, order = c(p, d, q), seasonal = list(order = c(P, D,
## Q), period = S), include.mean = !no.constant, transform.pars = trans, fixed = fixed,
## optim.control = list(trace = trc, REPORT = 1, reltol = tol))
##
## Coefficients:
## ma1 sma1
## -0.4734 -0.7861
## s.e. 0.0598 0.0451
##
## sigma^2 estimated as 47.4: log likelihood = -1211.28, aic = 2428.56
##
## $degrees_of_freedom
## [1] 358
##
## $ttable
## Estimate SE t.value p.value
## ma1 -0.4734 0.0598 -7.9097 0
## sma1 -0.7861 0.0451 -17.4227 0
##
## $AIC
## [1] 6.545975
##
## $AICc
## [1] 6.546062
##
## $BIC
## [1] 6.577399# Fit another model, this time with an AR
sarima(birth, p = 1, d = 1, q = 1, P = 0, D = 1, Q = 1, S = 12)## initial value 2.218186
## iter 2 value 2.032584
## iter 3 value 1.982464
## iter 4 value 1.975643
## iter 5 value 1.971721
## iter 6 value 1.967284
## iter 7 value 1.963840
## iter 8 value 1.961106
## iter 9 value 1.960849
## iter 10 value 1.960692
## iter 11 value 1.960683
## iter 12 value 1.960675
## iter 13 value 1.960672
## iter 13 value 1.960672
## iter 13 value 1.960672
## final value 1.960672
## converged
## initial value 1.940459
## iter 2 value 1.934425
## iter 3 value 1.932752
## iter 4 value 1.931750
## iter 5 value 1.931074
## iter 6 value 1.930882
## iter 7 value 1.930860
## iter 8 value 1.930859
## iter 8 value 1.930859
## final value 1.930859
## converged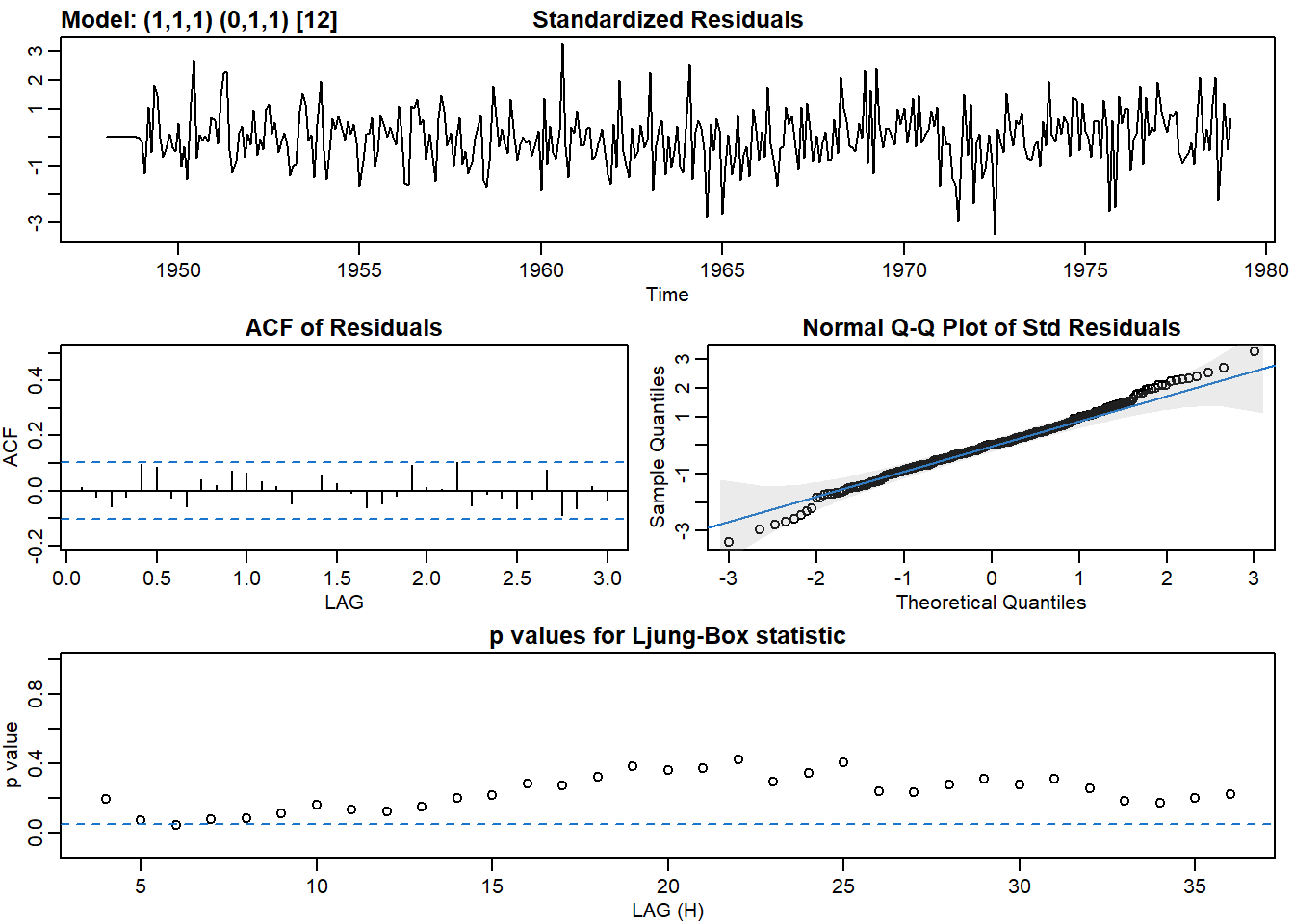
## $fit
##
## Call:
## stats::arima(x = xdata, order = c(p, d, q), seasonal = list(order = c(P, D,
## Q), period = S), include.mean = !no.constant, transform.pars = trans, fixed = fixed,
## optim.control = list(trace = trc, REPORT = 1, reltol = tol))
##
## Coefficients:
## ar1 ma1 sma1
## 0.3038 -0.7006 -0.8000
## s.e. 0.0865 0.0604 0.0441
##
## sigma^2 estimated as 45.91: log likelihood = -1205.93, aic = 2419.85
##
## $degrees_of_freedom
## [1] 357
##
## $ttable
## Estimate SE t.value p.value
## ar1 0.3038 0.0865 3.5104 5e-04
## ma1 -0.7006 0.0604 -11.5984 0e+00
## sma1 -0.8000 0.0441 -18.1302 0e+00
##
## $AIC
## [1] 6.522519
##
## $AICc
## [1] 6.522695
##
## $BIC
## [1] 6.564418